vcMatrix
vcMatrix is a 4x4 matrix and is generally used to perform linear transformations and contain the position and orientation of objects.
Constructors
| Name | Return Type | Parameters | Description |
| new | vcMatrix | [vcMatrix matrix] | Creates a new vcMatrix object. |
Operators
| Name | Description |
| * | Performs matrix multiplication with another vcMatrix object or transforms a vcVector object. If the multiplier is a vcVector object, the product will be a vcVector object. |
Properties
| Name | Type | Access | Description |
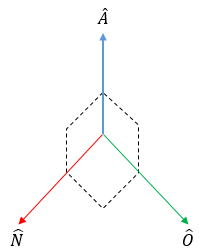
| N | vcVector | RW | Defines Normal vector that is unit vector in X-axis direction. |
| O | vcVector | RW | Defines Orientation vector that is unit vector in Y-axis direction. |
| A | vcVector | RW | Defines Approach vector that is unit vector in Z-axis direction. |
| P | vcVector | RW | Defines Position vector. |
| WPR | vcVector | RW | Defines roll, pitch and yaw angles. |
Note: The directional vectors N,O and A should be unit vectors and orthonormal. That is, the length of N,O and A should be 1.0, and they should be normal to one another (orthonormal). Otherwise, the vcMatrix object will be skewed.
Methods
| Name | Return Type | Parameters | Description |
| getAxisAngle | vcVector | None | Returns the orientation of the matrix as a rotation of its identity matrix about the axis defined by the XYZ values of the returned vector.
The W property of the returned vector is the rotation angle (in degrees). |
| getEuler | vcVector | None | Returns the orientation of the matrix as a set of absolute rotations (in fixed coordinate system) around the Z-axis, followed by the Y-axis, and then again the Z-axis, in the form of a vector containing those angles (in degrees). |
| getQuaternion | vcVector | None | Returns the orientation of the matrix as a quaternion in the form of a vector. |
| getWPR | vcVector | None | Returns the orientation of the matrix as a set of relative rotations around ZYX axes, in that order, in the form of a vector containing those angles (in degrees). |
| identity | None | None | Sets matrix to equal its identity. |
| invert | None | None | Sets the matrix to equal its inverse. |
| rotateAbsX | None | Real value | Rotates the matrix around X-axis in absolute coordinate system. |
| rotateAbsY | None | Real value | Rotates the matrix around Y-axis in absolute coordinate system. |
| rotateAbsZ | None | Real value | Rotates the matrix around Z-axis in absolute coordinate system. |
| rotateAbsV | None | vcVector v, Real angle | Rotates the matrix around an axis defined by a given vector by a given angle in absolute coordinate system. |
| rotateRelX | None | Real value | Rotates the matrix around X-axis in coordinate system relative to matrix position. |
| rotateRelY | None | Real value | Rotate the matrix around Y-axis in coordinate system relative to matrix position. |
| rotateRelZ | None | Real value | Rotates the matrix around Z-axis in coordinate system relative to matrix position. |
| rotateRelV | None | vcVector v, Real angle | Rotates the matrix around an axis defined by a given vector by a given angle in coordinate system relative to matrix position. |
| scaleAbs | None | Real x, Real y, Real z | Scales the matrix in relation to 3D world origin. |
| scaleRel | None | Real x, Real y, Real z | Scales the matrix in relation to matrix position. |
| setAxisAngle | None | Real x, Real y, Real z, Real w | Rotates the matrix around an axis.
The x, y and z arguments define a unit vector and direction of axis. The w argument defines the rotation (in degrees) around that axis. |
| setEuler | None | Real x, Real y, Real z | Sets the orientation of the matrix by executing a set of absolute rotations (in degrees) around Z-axis, followed by Y-axis, and then around Z-axis in fixed coordinate system. |
| setIJK | None | Real i, Real j, Real k | Sets the orientation of the matrix so that its Approach vector (Z-axis) is aligned with a vector defined by i, j and k arguments. |
| setQuaternion | None | Real q1, Real q2, Real q3, Real q4 | Sets the orientation of the matrix by using a quaternion defined by four given arguments. |
| setWPR | None | Real yaw, Real pitch, Real roll | Sets the orientation of the matrix by using roll, pitch and yaw arguments. |
| translateAbs | None | Real x, Real y, Real z | Translates the matrix position by a given offset (XYZ values) in reference (Parent) coordinate system. Parent can be for example the World or a Node. |
| translateRel | None | Real x, Real y, Real z | Translates the matrix position by a given offset (XYZ values) in Object coordinate system. |
| uniform | None | None | Modifies the matrix to be orthogonal and contain no scaling. |
Examples
Example. Create matrix position for component
| from vcScript import * import vcMatrix comp = getComponent() mtx = vcMatrix.new() mtx.translateRel(1000,500,500) mtx.rotateRelY(45) comp.PositionMatrix = mtx getApplication().render() |
Example. Manipulating and printing matrix values
| # create a python behaviour replace and compile import vcMatrix as mat def printMatrix(mat): """Usefull utility function for printing matrix value""" for Vec in [mat.N,mat.O,mat.A,mat.P]: print ("%3.3g\t%3.3g\t%3.3g\t%3.3g\n"%(Vec.X,Vec.Y,Vec.Z,Vec.W)) #lets generate a matrix m=mat.new() # rotate it in place m.rotateRelX(12.5) m.rotateRelZ(20) # Then move about m.translateRel(0,0,102) # please note following will not work # m.P.X=345 # use instead vec=m.P vec.X=345 m.P=vec # print the resulting matrix printMatrix(m) |
Example. Get object's position matrix in relation to another object's coordinate system
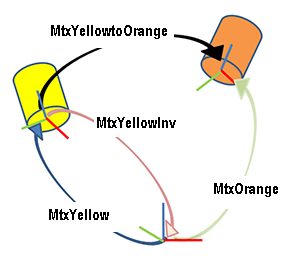
| from vcScript import * import vcMatrix app = getApplication() yellow = app.findComponent('Yellow') orange = app.findComponent('Orange') mtxOrange = orange.PositionMatrix #green arrow in the picture mtxYellow = yellow.PositionMatrix # blue arrow in the picture invMtxYellow = yellow.PositionMatrix invMtxYellow.invert() # purple arrow in the picture mtxYellowToOrange = invMtxYellow * mtxOrange # result: black arrow in the picture print mtxYellowToOrange.P.X,mtxYellowToOrange.P.Y,mtxYellowToOrange.P.Z |